A magic square consists of the distinct positive integers
If the rows and columns sum to the magic constant (so ignoring the main diagonals) it is called a semimagic square.
Several ways exist to automatically generate magic squares, among which the most famous one is the Siamese method to generate odd-sized magic squares. It is also called the de la Loubere's method. The method is purported to have been first reported in the West when de la Loubere returned to France after serving as ambassador to Siam.
This example is taken from the excellent description on Math Forum. I reproduce it almost literally here in case that link ever goes away.
Start with an empty n x n square, where n is odd. We'll begin with n = 5 and denote its blank entries with dots.
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
The problem of making this into a magic square is one of counting from 1 to 25 (in general n2) as one runs through the boxes of the square in some order. The basic rule for doing this is that one counts diagonally upwards to the right. For example, if one has written a 12 in the 2nd position of the 4th row
. . . . .
. . . . .
. . . . .
. 12 . . .
. . . . .
then the numbers 13,14,15 will be placed thus:
. . . . 15
. . . 14 .
. . 13 . .
. 12 . . .
. . . . .
Let's see this in action.First you have to know where to start: begin in the middle of the top row with a 1. (Here we for the first time use the assumption that n is odd, which guarantees that there is a middle square in the top row). If you don't start there, the row and column sums will be ok, but the diagonals won't add to the magic sum.
. . 1 . .
. . . . .
. . . . .
. . . . .
. . . . .
Now, the first thing one observes is that it is impossible to move diagonally upwards from this position, since we are already at the top of the square. This is an example of what can go wrong with the basic method of moving diagonally upwards to the right. There are actually three things that can go wrong:
-
You could be at the top edge of the square so you can't go up.
You could be at the right edge of the square so you can't move
right.
The square you would like to put the next number in may already
be occupied.
Here is what to do in those cases:
-
If you are at the top edge, pretend that the top edge is
pasted to the bottom edge and come up through the bottom. Thus,
after 1, we place 2 as follows:
. . 1 . .
. . . . .
. . . . .
. . . . .
. . . 2 .
In other words, we pretend that the bottom row is the row above the top
row. Moving diagonally upwards to the right means moving up one row and
over one column to the right. So the 2 goes in the bottom row one column
to the right of the column containing the 1.
If you are at the right edge, pretend that the right edge is pasted to the left edge and that the left edge is immediately to the right of the right edge. We are in this situation after counting to 3, since after the above diagram, we have
. . 1 . .
. . . . .
. . . . .
. . . . 3
. . . 2 .
and apparently have no place to go. But moving diagonally upwards to the
right is the same as moving right one column and up one row. Moving right
one column from the rightmost column puts us in the leftmost column, so 4
must be in the leftmost column, and moving up one row we put the 4 in the
row above the row containing the 3. So we get
. . 1 . .
. . . . .
4 . . . .
. . . . 3
. . . 2 .
What if there is a number already occupying the square one
would like to move into? We are in this situation after we place the
number 5. Indeed, continuing from the previous diagram, we place the 5
diagonally upwards and to the right of the 4 and get
. . 1 . .
. 5 . . .
4 . . . .
. . . . 3
. . . 2 .
and when we next try to place the 6, the square we would like to put the 6
in already has the 1 in it! When this happens, the rule is to abandon,
just this once, the plan of moving diagonally upwards to the right and
instead just drop down one square from the square one is in presently. So
the 6 will be placed directly below the 5.
. . 1 . .
. 5 . . .
4 6 . . .
. . . . 3
. . . 2 .
After that, one continues counting normally:
. . 1 8 .
. 5 7 . .
4 6 . . .
. . . . 3
. . . 2 .
Eventually, one gets the whole 5x5 square in this way:
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
The magic constant is 65 in this example, and indeed all rows, columns and
the two main diagonals sum to 65.
The application of the basic rule of counting diagonally upwards, with the modifications above for handling the edges and the case where a number is in the way, is pretty straightforward. But there is one case that requires a little thought. Namely, when one gets to 15, where does one go next?
. . 1 8 15
. 5 7 14 .
4 6 13 . .
10 12 . . 3
11 . . 2 9
Since 15 is in the top row, 16 would normally go in the bottom row. Since
15 is on the right edge, 16 would normally go on the left edge. The
position which is in the bottom row and the left edge is the lower left
corner. That is where we want to put the 16. Unfortunately, it is already
occupied by the number 11. So there is a number in the way, and the rule
is then to drop down to the square below the 15. That is why the 16 is
directly below the 15.
. . 1 8 15
. 5 7 14 16
4 6 13 . .
10 12 . . 3
11 . . 2 9
All other instances of the rules are a lot easier to figure out.
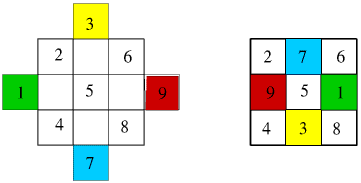
The same method was used to make a 3x3 magic square:
8 1 6
3 5 7
4 9 2
It is directly obvious that this construction is is really only one of a whole family. Instead of generating the diagonals going up/right, we could also have chosen to go down/left or up/left or down/right, appropiately changing the step we do when we come to an already filled in square.
But the family is more general in fact. Consider for example the follwing description of the pyramid method taken from Mathematics Enrichment.
The Pyramid method or extended diagonals consists of three steps:
- Draw a pyramid of same size squares as the magic square's squares, on each side of the magic square. The pyramid should be two less, in number of squares on its base, than the number of squares on the side of the magic square.
- Sequentially place the numbers 1 to n2 of the nxn magic square in the diagonals as shown in figure 1.
- Relocate any number not in the nxnsquare to the opposite hole inside the square (shaded).
The same Pyramid method can be used for any odd order magic square as shown below for the 5x5 square.
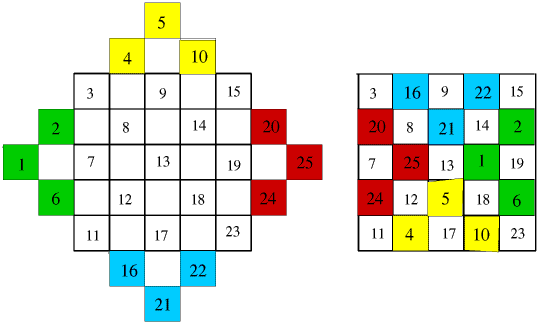
Now if you carefully observe the resulting magic squares, you see that it is in fact just the standard Siamese method, but with a different starting point (one to the right of the center) and another displacement in case a square is already occupied (go 2 to the right)
The standard dispacement also does not have to be a simple diagonal. Consider for example using a knights jump down right as standard move and moving up two as exceptional move:
10 12 19 21 3
17 24 1 8 15
4 6 13 20 22
11 18 25 2 9
23 5 7 14 16
However, not just everything works. Consider for example going one to the right as standard move and one down as exceptional move:
1 2 3 4 5
7 8 9 10 6
13 14 15 11 12
19 20 16 17 18
25 21 22 23 24
Here even the rows and columns don't sum to the magic constant, and it's
obvious that moving the starting point won't change this (you'll still end
up with a row containing a permutation of 1,2,3,4,5 and another row
containing a permutation of 21,22,23,24,25 which obviously don't have the
same sum).
So the question arises: what exactly are the rules ?
Let's denote the amount of times we applied the standard move by i (start counting at 0), and the amount of times we did the exceptional move by j (again start counting at 0). And let's apply a coordinate system to the square, where x runs from left to right and y runs from top to bottom, again both counting from 0. And let's call the x and y coordinates of the initial number a' and b' respectively. Let's also call the dispacements of the normal step in the x and y direction u' and v'.
So for the first few steps in the Siamese method we get something like:
x = i*u'+a'
y = i*v'+b'
In the first example we started in the middle of the top row, so with
x = i+(n-1)/2
y = -i
Oops, we already get into trouble at
x = (i*u'+a')%n
y = (i*v'+b')%n
In modular arithmetic it's directly obvious that
i0*f*(u'/f) = k*f*(n/f)
or
i0*(u'/f) = k*(n/f)
where u'/f has no factors in common with n/f (since
i*u = m *(n/f)*f*(u'/f) = m *n*(u'/f) = 0 (mod n)
i*u = m'*(n/f)*f*(v'/f) = m'*n*(v'/f) = 0 (mod n)
(So we see that
So each time i is a multiple of i0, we apply the exceptional case by adding and extra offset of p' and q' to x and y. So we get:
x = (i*u'+j*p'+a')%n
y = (i*v'+j*q'+b')%n
Notice that this is slightly different from the way we formulated the
exceptional displacement up to this point, since that used to be relative to
i0-1, so it correspondeds to (p'+u', q'+v'). This is
x = ( i-j+(n-1)/2)%n
y = (-i+2*j)%n
Again it is obvious that in general when j is a multiple of n, this is
equivalent to
It's also interesting to see that i and j are symmetrical, so at least for filling up the matrix it doesn't matter if you exchange the normal displacement with the exceptional displacement (we don't say anything yet about if that gives a magic square or not).
So we have for both i and j basically n different values [0..n-1]. And each of these n2 combinations gives a certain (x, y) coordinate where we fill in j*n+i+1. We also found a necessary condition for the (x, y) coordinates to be all different, but don't know yet if the condition is sufficient. A necessary and sufficient condition will in fact be if for every (x, y) we can find a (i, j) mapping to it. So let's try to invert the basic formula:
i*u'*q'+j*p'*q' = x*q'-a'*q' (mod n)
i*v'*p'+j*q'*p' = y*p'-b'*p' (mod n)
------------------------------------
i*(u'*q'-v'*p') = (x-a')*q'-(y-b')*p' (mod n)
and simularly:
j*(u'*q'-v'*p') = (y-b')*u'-(x-a')*v' (mod n)
This is obviously solvable if
i = ((x-a')*q'-(y-b')*p')/(u'*q'-v'*p') %n
j = ((y-b')*u'-(x-a')*v')/(u'*q'-v'*p') %n
or, after introducing new names for constants:
u = q'/(u'*q'-v'*p') (mod n)
v = -v'/(u'*q'-v'*p') (mod n)
p = -p'/(u'*q'-v'*p') (mod n)
q = u'/(u'*q'-v'*p') (mod n)
a = (b'*p'-a'*q')/(u'*q'-v'*p') (mod n)
b = (a'*v'-b'*u')/(u'*q'-v'*p') (mod n)
we get:
i = (x*u+y*p+a)%n
j = (x*v+y*q+b)%n
This is in fact of exactly the same form as we started from, so viewing
magic squares in the What if
i*g*((u'*q'-v'*p')/g) = (x-a')*q'-(y-b')*p' (mod n)
for every x and y. So if we take Let's quickly go back to the question if the conditions
gcd(n, u', v') = 1
gcd(n, p', q') = 1
are sufficient. Consider
x = 2*i + 7*j (mod 39)
y = 5*i +11*j (mod 39)
Multiplying the second by 7 and subtracting the first times 11 gives:
7*y - 11 *x = 13*j (mod 39)
So we see that the real reason is that the equations are not independent,
and so not all (x, y) combinations are allowed. For example when x is 0,
y must be 0, 13 or 26.
Let's go back to the original example:
x = i-j+(n-1)/2 (mod n)
y = -i+2*j (mod n)
So
i = 2*x+y+1 (mod n)
j = x+y-(n-1)/2 (mod n)
For another example we'll take the pyramid method, which we can write as:
x = i+j+(n+1)/2 (mod n)
y = -i+j+(n-1)/2 (mod n)
So
i = (x-y-1)*(n+1)/2 (mod n)
j = (x+y )*(n+1)/2 (mod n)
This case is particularly interesting since it shows an example of
displacements that are not a constant, but multiples of (n+1)/2. And due
to the duality this makes us suspect that displacements of this form can
also be used in the Siamese method (this suspicion will turn out to be
true. You can get magic squares like that). Also notice that
So now let's consider:
value(x, y) = i+j*n
where:
i = (x*u+y*p+a)%n
j = (x*v+y*q+b)%n
and:
gcd(u*q-p*v, n) = 1
Notice that I sneakily subtracted one from the value. This doesn't really
matter, since subtracting one from every value in the square makes
no difference whatsoever to the magicness or semi-magicness of a square
(though it changes the value of the magic constant obviously).
We know that all magic squares generated with the Siamese method are of this form. What about the other direction ? Due to the invertability, we know that all values from 1 to n2 will appear in the generated square. But obviously it's not always magic, for example:
i = x%n
j = y%n
Leads to this very obviously non-magic square:
0 1 2 3 4
5 6 7 8 9
10 11 12 13 14
15 16 17 18 19
20 21 22 23 24
Clearly we must demand that the sum of the rows and columns gives the
magic constant.
Let's first determine this magic constant. The total sum of all
elements in the square is obviously the mean value times the number of
elements, so
S = TotalSum/n = n*(n2-1)/2 = n*(n-1)*(n+1)/2 = n * [n*(n-1)/2 + (n-1)/2]
Next let's get rid of that
0 = x0*u+y0*p+a (mod n)
0 = x0*v+y0*q+b (mod n)
which we subtract from the basic formula to get:
i = (x-x0)*u+(y-y0)*p (mod n)
j = (x-x0)*v+(y-y0)*q (mod n)
This basically corresponds to taking off the top x0 rows of the square and
reattaching them to the bottom, and removing the left y0 rows and attaching
them to the right. This obviously does not change either the row or column
sums (though it does change the diagonals). So since we are only going
to demand semi-magicness in this section, it's enough to study:
value(x, y) = i+j*n
where:
i = x*u+y*p (mod n)
j = x*v+y*q (mod n)
and:
gcd(u*q-p*v, n) = 1
Let's fix
i 0 u%n 2*u%n .... (n-1)*u%n
j 0 v%n 2*v%n .... (n-1)*v%n
If we denote the sum over n multiples of u with sum(u, n), we get as
condition for the total rowsum:
S = n * (n * (n-1)/2) + (n * (n-1)/2) = n * sum(v, n) + sum(u, n)
So we are led to study the sum of sequences of the form:
0 u%n 2*u%n .... (n-1)*u%n
The key question to ask here is if any of these values (after the first one)
will be 0. Let's assume that the first multiplier for which this happens
is m and that
gcd(u/µ, n/µ) = 1
m*µ*(u/µ) = k * µ * (n/µ)
m*(u/µ) = k * (n/µ)
All factors of n/µ are not in u/µ, so they must appear in
m, so m is a multiple of n/µ. In the same way k must be a multiple of
u/µ, so the smallest solution is
m = n/µ
k = u/µ
So the sequence to sum will look like:
gcd(u, n) = µ
U = u/µ
N = n/µ
gcd(U, N) = 1
µ times (0 U*µ%n 2*U*µ%n .. (N-1)*U*µ%n)
For example, if
0 4 2 0 4 2
Which is indeed 2 times
0 2*2%6 2*2*2%6
0 4 2
So now let's consider one such subsequence. We can obviously divide out the common factor µ to get the sequence:
0 U%N 2*U%N .... (N-1)*U%N
Which in the example indeed corresponds to
0 2 1
where each element then has to be multiplied by
Since it will in fact be a permutation, there will be a 1 in the sequence,
so there exists an m such that
At this point we have all we need to work out the general sum. First the sequence with the factor µ divided out:
sum = 0 1 2 .... N-1 (writing the sequence forward)
sum = N-1 N-2 N-3 .... 0 (writing the sequence backward)
----------------------------
2*sum = N-1+N-1+N-1 .... N-1 = N*(N-1)
sum = N*(N-1)/2
So adding back the µ factor and that we have this sequence µ
times gives:
sum(u, n) = µ2 * N * (N-1)/2 = µ2 * (n/µ) * ((n/µ)-1)/2 = n * (n-µ)/2
Notice that this is always less or equal to
S = n * (n * (n-1)/2) + (n * (n-1)/2) = n * sum(v, n) + sum(u, n)
shows We've also proven that if
And applying the same reasoning to j gives that all column sum to the
magic constant if and only if
Notice that at this point we haven't really used yet that n is odd.
So can this method lead to even squares ? Since u, v, p and q must be
relatively prime to n, all of them must be odd. but then
So now let's consider:
value(x', y') = i+j*n
where:
i = (x'*u+y'*p+a')%n
j = (x'*v+y'*q+b')%n
and:
gcd(u*q-p*v, n) = 1
gcd(u, n) = gcd(v, n) = gcd(p, n) = gcd(q, n) = 1
We know that every magic square generated with the Siamese method is of this
form. What about the other direction ? Due to the invertability we know that
every value will appear in the resulting magic square. Due to the conditions
on u, v, p and q we know that all sums and rows sum to the magic constant.
What remains is to study the diagonals.
The two diagonals meet in the center. To make the situation more symmetric, we will move the (x, y) coordinates so that (0, 0) is the center. So we introduce
x = x'-(n-1)/2 (mod n)
y = y'-(n-1)/2 (mod n)
so:
i = (x+(n-1)/2)*u+(y+(n-1)/2)*p+a' = x*u+y*p+(a'+(u+p)*(n-1)/2) (mod n)
j = (x+(n-1)/2)*v+(y+(n-1)/2)*q+b' = x*v+y*q+(b'+(v+q)*(n-1)/2) (mod n)
So by defining
a = a'+(u+p)*(n-1)/2 (mod n)
b = b'+(v+q)*(n-1)/2 (mod n)
We get the familiar:
value(x, y) = i+j*n
where:
i = (x*u+y*p+a)%n
j = (x*v+y*q+b)%n
and:
gcd(u*q-p*v, n) = 1
gcd(u, n) = gcd(v, n) = gcd(p, n) = gcd(q, n) = 1
So let's run x and y from -(n-1)/2 to (n-1)/2. We get the following sequences
i: [-(n-1)/2*(u+p)+a]%n, [(1-(n-1)/2)*(u+p)+a]%n .... a%n .... [((n-1)/2-1)*(u+p)+a]%n [(n-1)/2*(u+p)+a]%n
j: [-(n-1)/2*(v+q)+b]%n, [(1-(n-1)/2)*(v+q)+b]%n .... b%n .... [((n-1)/2-1)*(v+q)+b]%n [(n-1)/2*(v+q)+b]%n
Let's denote the sum of the i sequence as sum(u+p, a, n), then we get for
this diagonal:
S = n * (n * (n-1)/2) + (n * (n-1)/2) = n * sum(v+q, b, n) + sum(u+p, a, n)
For the other diagonal we let x run from -(n-1)/2 to (n-1)/2 while y runs from (n-1)/2 to -(n-1)/2. This gives:
i: [-(n-1)/2*(u-p)+a]%n, [(1-(n-1)/2)*(u-p)+a]%n .... a%n .... [((n-1)/2-1)*(u-p)+a]%n [(n-1)/2*(u-p)+a]%n
j: [-(n-1)/2*(v-q)+b]%n, [(1-(n-1)/2)*(v-q)+b]%n .... b%n .... [((n-1)/2-1)*(v-q)+b]%n [(n-1)/2*(v-q)+b]%n
so
S = n * (n * (n-1)/2) + (n * (n-1)/2) = n * sum(v-q, b, n) + sum(u-p, a, n)
So this time we study a sequence of the form
(-(n-1)/2*u+a)%n, ((1-(n-1)/2)*u+a)%n, ... (-u+a)%n, a%n, (u+a)%n, ... (((n-1)/2-1)*u+a)%n, ((n-1)/2*u+a)%n
It will be interesting to see if the value
(-k*u+a)%n, ((1-k)*u+a)%n, .... (-u+a)%n, a%n, (u+a)%n, ... ((k-1)*u+a)%n, (k*u+a)%n
which will appear µ times. Since we want to try to get rid of a factor
µ again, let's write a as
(-k*U*µ+å*µ+A)%n, ((1-k)*U*µ+å*µ+A)%n, .... (-U*µ+å*µ+A)%n, å*µ+A%n, (U*µ+å*µ+A)%n, ... ((k-1)*U*µ+å*µ+A)%n, (k*U*µ+å*µ+A)%n
This sequence consists of multiples of µ (which divides n) plus A
where
(-k*U*µ+å*µ)%n+A, ((1-k)*U*µ+å*µ)%n+A, .... (-U*µ+å*µ)%n+A, å*µ%n+A, (U*µ+å*µ)%n+A, ... ((k-1)*U*µ+å*µ)%n+A, (k*U*µ+å*µ)%n+A
So if we remove n times A from the elements of the sequence, we get
(-k*U*µ+å*µ)%n, ((1-k)*U*µ+å*µ)%n, .... (-U*µ+å*µ)%n, å*µ%n, (U*µ+å*µ)%n, ... ((k-1)*U*µ+å*µ)%n, (k*U*µ+å*µ)%n
Which is of the form we already handled, and equals sum(u, n) (the å
additions again only cause an extra permutation, but do not change the sum).
So
sum(u, a, n) = sum(u, n) + n * A = n*(n-µ)/2+n*A = n*(n+2*A-µ)/2
So the demand that:
S = n * (n * (n-1)/2) + (n * (n-1)/2) = n * sum(v+q, b, n) + sum(u+p, a, n)
leads us to consider:
n * (n * (n-1)/2) + (n * (n-1)/2) = n * (n*(n+2*B-ð)/2) + n*(n+2*A-µ)/2
n * (2*B-ð+1) + (2*A-µ+1) = 0
Let's consider 2*A-µ+1. The possible values of A are in
[0..µ-1], so the possible values of this run in
[-(µ-1)..µ-1] and
2*A-µ+1 = 0
2*B-ð+1 = 0
or, if we consider it our job to determine a and b once u, v, p and q are
known:
A = (µ-1)/2
B = (ð-1)/2
Each diagonal will lead to a condition of this kind. They must of course be
compatible.
Let's recap what we worked out in the previous section:
µ = gcd(u+p, n)
A = a%µ
ð = gcd(v+q, n)
B = b%ð
2*A = µ-1
2*B = ð-1
µ' = gcd(u-p, n)
A' = a%µ'
ð' = gcd(v-q, n)
B' = b%ð'
2*A' = µ'-1
2*B' = ð'-1
So the compatibility conditions become:
a = s * µ + A = s' * µ' + A'
b = t * ð + B = t' * ð' + B'
with s, s', t and 't integers
s * µ + A = s' * µ' + A'
s * µ + (µ-1)/2 = s' * µ' + (µ'-1)/2
(2*s+1)*µ = (2*s'+1)*µ'
So we must find out more about So each factor of µ' must appear in 2*s+1, and each factor of µ must appear in 2*s'+1, so:
2*s'+1 = (2*k+1) * µ
2*s+1 = (2*k+1) * µ'
With k an integer (we know the factor is odd because 2*s'+1 is odd). So:
a = s * µ + (µ-1)/2 = ((2*s+1)*µ-1)/2 = ((2*k+1)*µ*µ'-1)/2 = k*µ*µ'+(µ*µ'-1)/2
Formulating a in terms of µ' leads to the same formula, so we found
the necessary and sufficient condition for compatibility of a. And in the
same way we find:
b = ((2*l+1)*ð*ð'-1)/2 = l*ð*ð'+(ð*ð'-1)/2
And translating back to (x, y) we see:
a' = ((2*k+1)*µ*µ'-1)/2-(u+p)*(n-1)/2 = k'*µ*µ'+(1-u-p)*(µ*µ'-1)/2
b' = ((2*l+1)*ð*ð'-1)/2-(v+q)*(n-1)/2 = l'*ð*ð'+(1-v-q)*(ð*ð'-1)/2
In the last step I used that So the final conclusion is that we get a magic square generated with the Siamese method if and only if:
value(x, y) = i+j*n
where:
i = (x*u+y*p+k*µ*µ'+(1-u-p)*(µ*µ'-1)/2)%n
j = (x*v+y*q+l*ð*ð'+(1-v-q)*(ð*ð'-1)/2)%n
and:
gcd(u*q-p*v, n) = gcd(u, n) = gcd(v, n) = gcd(p, n) = gcd(q, n) = 1
µ = gcd(u+p, n)
µ' = gcd(u-p, n)
ð = gcd(v+q, n)
ð' = gcd(v-q, n)
and k and l are arbitrary integers.
We can also write i and j as:
i = ((2*x-n+1)*u+(2*y-n+1)*p+(2*k'+1)*µ*µ'-1)/2%n
j = ((2*x-n+1)*v+(2*y-n+1)*q+(2*l'+1)*ð*ð'-1)/2%n
Let's first consider the original example again.
(u, v, p, q) = (2, 1, 1, 1)
µ = gcd(3, n)
µ' = gcd(1, n) = 1
ð = gcd(2, n) = 1
ð' = gcd(0, n) = n
So we must distinguish two cases:
gcd(n, 3) = 1 i = (2*x+y+k')%n j = (x+y-(n-1)/2)%ngcd(n, 3) = 3 orn = 3*(2*m+1) i = (2*x+y+3*k'+1)%n j = (x+y-(n-1)/2)%n
i = (2*x+y+3*k'+1)%n
j = (x+y-(n-1)/2)%n
In the previous case it was very interesting that the i formula had an almost arbitrary offset. It was in a way caused by µ and µ' being small constants. Let's try to get that effect on both i and j:
(u, v, p, q) = (2, 2, 1, -1)
det = u*q-v*p = -2-2 = -4, which is prime relative to all odd numbers, so the square will be magic.
µ = gcd(3, n)
µ' = gcd(1, n) = 1
ð = gcd(1, n) = 1
ð' = gcd(3, n)
Again we must distinguish two cases:
gcd(n, 3) = 1 i = (2*x+y+k')%n j = (2*x-y+l')%ngcd(n, 3) = 3 orn = (2m+1)*3 i = (2*x+y+3*k'+1)%n j = (2*x-y+3*l')%n
i = (2*x+y+3*k'+1)%n j = (2*x-y+3*l')%nIf we for example take
5 12 24 6 18
21 8 20 2 14
17 4 11 23 10
13 25 7 19 1
9 16 3 15 22
It's interesting to note that the average value, 13, does not appear in
the center.
So what if we decided to move the 13 to the center ? We can take two columns from the right side and reattach them at the left, and take one row from the top and attach it to the bottom. This sort of operation would obviously not impact the semi-magicness of the square, but it might disturb the diagonals, so the result might not be a magic square.
In the example under consideration 2 would move to the top left, and this
fact of course completely determines this "translation". In
general, we can decide to move the number at
i = x*u+y*p+a (mod n)
j = x*v+y*q+b (mod n)
x' = x-x0 (mod n)
y' = y-y0 (mod n)
to
i = (x'+x0)*u+(y'+y0)*p+a = x'*u+y'*p+(a+x0*u+y0*p) = x'*u+y'*p+a' (mod n)
j = (x'+x0)*v+(y'-y0)*q+b = x'*v+y'*q+(b+x0*v+y0*q) = x'*v+y'*q+b' (mod n)
a' = a+x0*u+y0*p (mod n)
b' = b+x0*v+y0*q (mod n)
(I used the So if we choose the average value in the center and use a coordinate
system with
i = (x*u+y*p+k*n+(n-1)/2)%n
j = (x*v+y*q+l*n+(n-1)/2)%n
(I left in the k and l to stress the complete set of solutions. In
practise they of course have no influence and you just drop them).
If you now consider two points in positions symmetric with respect
to the center, their x and y coordinates have opposite sign, so equally
much gets added or subtracted from (n-1)/2. And since 0 an n-1 are
equally far from (n-1)/2, if the modulo wraps -1 or lower up, the other
position is at n or higher and gets wrapped down equally much. So the sum
of the values at symmetric positions is constant, and in fact twice the
average (and now central) value,
In fact, a square is called "associative" if all positions
symmetric to the center sum to
And since the whole square is on average filled with the average value and all pairs (except the center) sum to twice the average value, every associative semi-magic square must have the average value in the center, so the two conditions are equivalent for siamese squares.
Using that
a = ((2*k+1)(2*M+1)*µ*µ'-1)/2
b = ((2*l+1)(2*E+1)*ð*ð'-1)/2
which is compatible with the condition for the diagonals to sum to
the magic constant, so every associative semi-magic Siamese square is
magic. So moving the average value to the center in the example in fact
didn't destroy the magicness. On the contrary, it's a way you can make any
semi-magic Siamese square magic.
Translating back to zero-based coordinates for
i = (x*u+y*p+(1-u-p)*(n-1)/2)%n
j = (x*v+y*q+(1-v-q)*(n-1)/2)%n
Going back to our standard example
i = (2*x+y+1)%n
j = ( x+y-(n-1)/2)%n
which is the exact formula we found for the example inversions. So
the classic construction gives associative magic squares.
The other example we recently looked at was
i = (2*x+y+1)%n
j = (2*x-y)%n
Notice how choosing u+p and v+q to be odd tends to get rid of the ugly
offsets.
When all the diagonals, including those obtained by "wrapping around" the edges, of a magic square sum to the same magic constant, the square is said to be a panmagic square.
In this example from MathWorld you see at the left the normal magic square condition and to the right the conditions for all wrapped diagonals (in both directions):
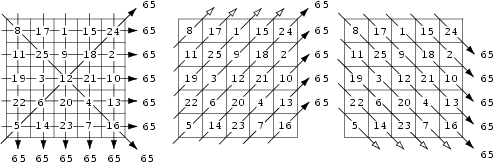
If you go back to the sequences we studied when demanding a square is magic, it's easy to see that e.g. moving z times one down from the main diagonal corresponds to adding z*p to the i entries and z*q to the j entries. Each of these must give a component of the magic constant (We only demanded that all diagonals sum to the same value, but since in this way we cover all positions, this value must be the magic constant. And the diagonal compatibility condition will also be fullfilled). So:
n * (n-1)/2 = sum(u+p, a+z*p, n) = sum(u+p, n) + (a+z*p)%µ * n
n * (n-1)/2 = sum(v+q, a+z*q, n) = sum(v+q, n) + (a+z*q)%ð * n
(moving the diagonals to the right instead of down would correspond to
adding z*u and z*v and will of course lead to the same conclusions, since
in the end they represent the same diagonals). Since each of these must
give the same result irrespective of z, it follows that
µ = µ' = ð = ð' = 1
So a Siamese square is panmagic if and only if:
value(x, y) = i+j*n
where:
i = (x*u+y*p+k)%n
j = (x*v+y*q+l)%n
and:
gcd(u*q-p*v, n) = 1
gcd(u, n) = gcd(v, n) = gcd(p, n) = gcd(q, n) = 1
gcd(u+p, n) = gcd(u-p, n) = gcd(v+q, n) = gcd(v-q, n) = 1
and k and l are arbitrary integers.
We can easily make the square associative too by choosing k and l so that
they are of the form we determined higher.
Looking again at the examples, we see that
Considering
i = (2*x+y+k)%n
j = (2*x-y+l)%n
are panmagic if n is not a multiple of 3, so of the form
What happens in the previous example is pretty typical. Siamese squares
that are a multiple of 3 never seem to be panmagic. Why ? u+p, u-p, u and
p may obviously not be multiples of 3, otherwise their gcd with n is at
least 3, so
In a size n square, we can write each value as a+n*b with
i = (2*x+y+4)%n j = (2*x-y)%nthe following decomposition:
4 11 23 5 17 4 1 3 0 2 0 10 20 5 15
20 7 19 1 13 0 2 4 1 3 20 5 15 0 10
16 3 10 22 9 = 1 3 0 2 4 + 15 0 10 20 5
12 24 6 18 0 2 4 1 3 0 10 20 5 15 0
8 15 2 14 21 3 0 2 4 1 5 15 0 10 20
or, if we divide out the factor 5 in the last square we get these two
patterns:
4 1 3 0 2 0 2 4 1 3
0 2 4 1 3 4 1 3 0 2
1 3 0 2 4 3 0 2 4 1
2 4 1 3 0 2 4 1 3 0
3 0 2 4 1 1 3 0 2 4
These two squares of course correspond to the i and j squares since
the values in a Siamese square are i+n*j. One possible name for this
kind of regular patterns with repeated values is
"magic carpets".
In for example the i square you can clearly see how moving to the right each time adds u (2), while moving down each time adds p (1). Moving along the diagonal from top-left to bottom-right adds u+p (3), while moving from bottom-left to top-right adds u-p (1). In the j square moving to the right adds v (2), while moving down adds q(-1) and the diagonals add v+q and v-q, all of this modulo 5 of course.
But we in fact studied this kind of sequence already when calculating
sums over it. In particular, we studied when the patterns repeats, which
didn't happen if the step was relatively prime to n. And since
E B D A C a c e b d
A C E B D e b d a c
B D A C E d a c e b
C E B D A c e b d a
D A C E B b d a c e
And writing the two together gives a so-called
"Graeco-Latin square" (normally written with greek and latin
letters, but since most greek letters aren't in latin-1, i use upper- and
lowercase letters:
Ea Bc De Ab Cd
Ae Cb Ed Ba Dc
Bd Da Ac Ce Eb
Cc Ee Bb Dd Aa
Db Ad Ca Ec Be
which gives us another way to represent a semi-magic square.
Demanding that the diagonals don't repeat any value in the i square
corresponds to
Another condition that was needed for a magic square was that each
As an application consider the following (non Siamese of course) 4x4 panmagic square:
0 7 12 11
13 10 1 6
3 4 15 8
14 9 2 5
which has the interesting extra property that each sub 2x2 square (even when
wrapping over the edges) adds to the magic constant, for example
So consider a rectangular window of size w x h which would give the same sum of values wherever you place it (including wrapping). Choose a certain value in the j square, and consider all the position of this value as places to put the top-left corner of the rectangle. Fixing this value fixes all the j-value in all other positions in the rectangle since moving right is adding v and moving down is adding q (modulo n). so the complete j contribution is fixed.
In the i square, we now have the rectangle positioned with each
possible value once in the upper-left corner, and this value again fixes
all other i entries by the constant offsets u and p. Now consider the
two i-rectangles with for example 0 and 1 in the upper-left corner. All
values in the second rectangle are one higher than in the first rectangle,
except for any cases of n-1, which would become n and wrap to 0. So if
the first rectangle has z times n-1, we find that we add 1 w*h times and
subtract z times n when going from the first rectangle to the second. And
the sum must remain constant, so
Now consider two rectangles shifted by 1 down, for example:
x x x . . . . . . .
x x x . . X X X . .
x x x . . X X X . .
. . . . . X X X . .
. . . . . . . . . .
Since both rectangles contain the exact same set of values (w*h/n times
every
value), the row that gets removed from the top must be a permutation of the
row that gets added at the bottom. So subrows of width w at a distance h
from each other are each others permutations. Now consider two such subrows
shifted by 1 right:
x1 x2 x3 . . . X2 X3 X4 .
. . . . . . . . . .
. . . . . . . . . .
x5 x6 x7 . . . X6 X7 X8 .
. . . . . . . . . .
The top subrow of x's is a permutation of the bottom subrow. The same for
the two subrows of X's. Going from the left pattern to the right, at the
top we remove x1 and add X4. And at the bottom we remove x5 and add X8.
So there are two possibilities:
- x1 is the same as X4
Since every value appears only once on every row, this means that the subrow must in fact be the whole row (possibly multiple times). Sow=k*n is a trivial solution (of course the bottom is also the whole row, andx5 = X8 ). - x1 is different from X4
In that case the same thing must have gotten removed and added at the bottom, sox1 = x5 andX4 = X8 . Which, due to the uniqueness of values in a column, means that the height is a full column (or a multiple), so again we have a trivial solutionh = l*n .
A very simple exercise is to prove that the following shape has a constant sum in every 5x5 panmagic Siamese quare:
. . x . .
. x x x .
. . x . .
. . . . .
. . . . .